
Zadanie Tort (tor)
Pomóż nam usprawnić bazę zadań!
Tort
Limit pamięci: 64 MB
Bajtek obchodzi dzisiaj swoje urodziny. Zdmuchnął już wszystkie świeczki z tortu urodzinowego oraz podzielił go na 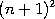 kawałków.
Niestety zrobił to w taki sposób, że kawałki tortu są teraz różnych wielkości, niektóre kawałki są większe, a inne mniejsze od pozostałych.
Bajtek wybiera swój kawałek jako pierwszy i chciałby wybrać
kawałków.
Niestety zrobił to w taki sposób, że kawałki tortu są teraz różnych wielkości, niektóre kawałki są większe, a inne mniejsze od pozostałych.
Bajtek wybiera swój kawałek jako pierwszy i chciałby wybrać 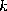 -ty pod względem wielkości, czyli taki, w którym
-ty pod względem wielkości, czyli taki, w którym 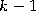 kawałków jest nie mniejszych od niego, a
kawałków jest nie mniejszych od niego, a 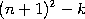 kawałków jest nie większych.
kawałków jest nie większych.
Wiemy, że tort urodzinowy Bajtka ma kształt prostokąta oraz że podzielił go  prostymi cięciami wzdłuż jednego z boków prostokąta i
prostymi cięciami wzdłuż jednego z boków prostokąta i  prostymi cięciami wzdłuż drugiego z boków. Chcielibyśmy znać powierzchnię wybranego przez Bajtka kawałka tortu.
prostymi cięciami wzdłuż drugiego z boków. Chcielibyśmy znać powierzchnię wybranego przez Bajtka kawałka tortu.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się cztery liczby całkowite 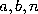 oraz
oraz 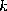 pooddzielane pojedynczymi odstępami (
pooddzielane pojedynczymi odstępami (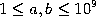 ,
, 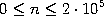 ,
,  ), oznaczające odpowiednio długości dwóch boków tortu, liczbę cięć wykonanych przez Bajtka w każdym z kierunków oraz numer szukanego kawałka.
), oznaczające odpowiednio długości dwóch boków tortu, liczbę cięć wykonanych przez Bajtka w każdym z kierunków oraz numer szukanego kawałka.
Drugi wiersz zawiera ciąg  liczb całkowitych
liczb całkowitych 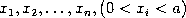 , gdzie
, gdzie 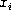 oznacza miejsce
oznacza miejsce 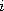 -tego cięcia wzdłuż jednego z boków prostokąta (jest to odległość od lewego boku prostokąta). Ponadto zachodzi
-tego cięcia wzdłuż jednego z boków prostokąta (jest to odległość od lewego boku prostokąta). Ponadto zachodzi 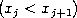 dla
dla 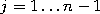 .
.
Trzeci wiersz zawiera ciąg  liczb całkowitych
liczb całkowitych 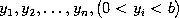 , gdzie
, gdzie  oznacza miejsce
oznacza miejsce 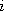 -tego cięcia wzdłuż drugiego z boków prostokąta (jest to odległość od dolnego boku prostokąta). Ponadto zachodzi
-tego cięcia wzdłuż drugiego z boków prostokąta (jest to odległość od dolnego boku prostokąta). Ponadto zachodzi 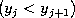 dla
dla 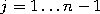 .
.
Możesz założyć, że w testach wartych co najmniej 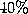 punktów zachodzi dodatkowy warunek:
punktów zachodzi dodatkowy warunek: 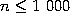 .
.
Wyjście
Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą, równą powierzchni 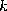 -tego pod względem wielkości kawałka tortu.
-tego pod względem wielkości kawałka tortu.
Przykład
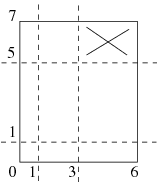
Dla danych wejściowych:
6 7 2 3 1 3 1 5
poprawną odpowiedzią jest:
6
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English